Gravity

masses =

Things fall. Pencils, buildings, people, everything falls. The Earth is falling towards the Sun, but luckily it is falling in a way that doesn't hit the Sun.
An orbit.

Early Theories of Gravity

The history of gravity tells the story of humanity realizing we aren't the center of the universe.

The Greek philosopher Aristotle (384–322 BCE) believed that the natural place for the element of earth and water was down. The natural place for the elements of air and fire was up. He also believed that heavier objects fell faster than light objects.

Like many early philosophers, Aristotle organized the sky into a geocentric model. Moving planetary spheres surrounded a stationary and spherical Earth.

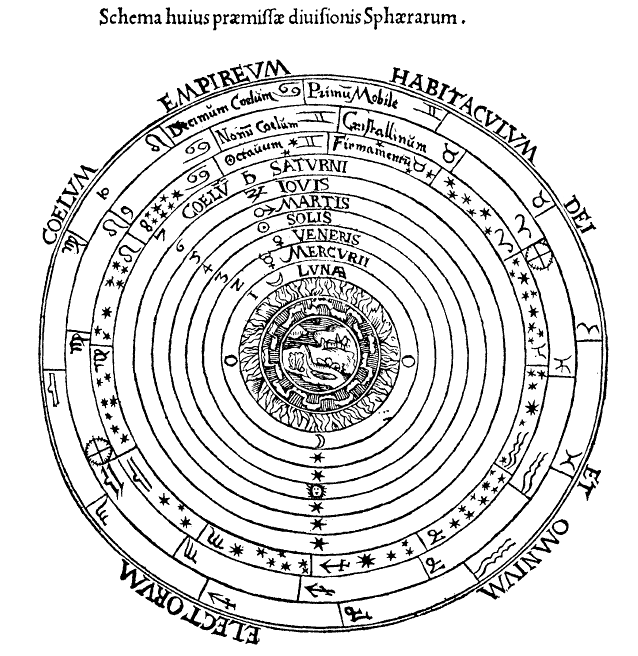
The geocentric models showed flaws. Planets would inexplicably change in speed and direction. To correct these flaws several small circles called epicycles were added to the path of the planets. As telescopes and data collection methods improved, the number of epicycles grew to correct for flaws in the geocentric model.

In 1543, Polish astronomer, Nicolaus Copernicus published a book on the heliocentric theory, the idea that the planets revolved around the Sun, not the Earth. His heliocentric theory marks the beginning of the scientific revolution.

Italian natural philosopher, Galileo Galilei, discovered that falling objects all accelerate at the same rate as long as air resistance isn't a significant factor.

Galileo also championed the heliocentric model even though it contradicted Catholic scripture. The leaders of the church asked him not to publish information that supported the heliocentric model, but Galileo continued. In response, the church forced him to recant his findings, they banned his work, and they sentenced him to house arrest from 1633 until his death in 1642.

Question: What advantages did the heliocentric model have over the geocentric model?
solution

At the time it wasn't clear what model was the best one, but the heliocentric model explained the world in a more elegant and simple way. Issues like retrograde motion of planets was explained naturally in the heliocentric model without the need for epicycles.

One of the reasons Galileo liked the heliocentric model was that he had observed the Venus went through phases, just like the moon. In the Ptolemaic model, where Venus orbits the Earth, it wouldn't go through the full cycle of phases.

The heliocentric model was actually less accurate than the geocentric model. This is because the geocentric model was using a series of epicycles to improve on the circular paths both models used. Eventually, Kepler's Laws showed that with elliptical paths the heliocentric model was more accurate.

Kepler's Laws of Planetary Motion

In 1609, German astronomer, Johannes Kepler published 3 laws of planetary motion based on the heliocentric theory.

planet F 2 A 1 A 2 F 1
  1. The orbit of a planet is an ellipse with the Sun at one of the two foci. (F1, F2)
  2. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. (A1 = A2)
  3. The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

$$ T^2 = r^3$$

\(T\) = orbital period, total time for one orbit [yr, years]
\(r\) = semi-major axis [AU, astronomical units, 1.5 × 1011 meters]

Kepler's laws mostly agreed with the Copernican model, but with a few improvements. In Kepler's model orbits moved in an ellipse, not a circle. The Sun wasn't the center of a planetary orbit, it was a foci of an elliptical orbit. Also, the planets would speed up and slow down as they orbited.

The semi-major axis of an ellipse is the distance from the center to the longest edge. For the Earth that distance is 149 597 870 700 m, which is called 1 astronomical unit (AU).

semi-major axis semi-minor axis ellipse The orbital period squared equals the semi-major axis cubed for units of years (yr) and astronomical units (AU). The relationship is more complex with other units.
modified equation for units of meters and seconds $$T^2 = \frac{4 \pi^2}{GM} r^3$$

\(T\) = orbital period, total time for one orbit [yr, years]
\(r\) = semi-major axis [AU, astronomical units, 1.5 × 1011 meters]
\(M\) = Mass of central body [kg, kilograms]
\(G\) = 6.67408 × 10-11 = universal gravitation constant [N m²/kg²]

planet semi-major axis orbital period
Mercury 0.387 AU 0.240 yr
Venus 0.723 AU 0.615 yr
Earth 1.000 AU 1.000 yr
Mars 1.524 AU
Jupiter 5.204 AU 11.86 yr
Saturn 9.582 AU 29.46 yr
Uranus 19.22 AU 84.02 yr
Neptune 30.11 AU 164.8 yr
Example: Calculate the time it takes Mars to orbit the Sun in years.
solution $$T^2 = r^3$$ $$T^2 = (1.524)^3$$ $$T^2 = 3.540$$ $$T = 1.88 \, \mathrm{yr}$$

Each planet in the solar system lands somewhere on this graph. So this graph tells us that the farther a planet is from the sun, the longer it takes to orbit. A Jupiter year is much longer than an Earth year.

Universal Gravitation

In 1687 Isaac Newton published his book, Mathematical Principles of Natural Philosophy. The book contained his laws of motion and his law of universal gravitation. His reasoning was based on geometric proofs and his new mathematical techniques which are now called calculus.

Universal gravitation states that every particle in the universe is attracted to every other particle. It connects the heavens and the Earth with one equation. The same force that makes apples fall also controls the motion of stars, planets, and moons.

M 1 M 2 F r

$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$

\(F\) = force of gravity [N, newtons, kg m/s²] vector
\(G\) = 6.67408 × 10-11 = universal gravitation constant [N m²/kg²]
\(M\) = mass [kg, kilograms]
\(r\) = distance between the center of each mass [m, meters]

M 1 M 2 F

Universal gravitation improved on Kepler's laws of planetary motion because it had a more universal application. Kepler's laws only applied to orbits where one body was much more massive, like the Sun and it's planets. Newton's gravitation applied to all matter.

No current theory perfectly describes reality. They all have the potential for improvement. In 1915 universal gravitation was improved on by Einstein's general relativity. It is hoped that one day we will improve on general relativity by combining it with quantum mechanics.

Each mass feels an equal but opposite force as predicted by Newton's 3rd law. This means that the same force of gravity you feel towards the Earth, the Earth feels towards you.

Question: Why don't we observe the Earth accelerating towards you?
answer

The Earth and you both have the same force, but not the same acceleration.

$$F=ma$$ $$a = \frac{F}{m}$$

Acceleration equals force divided by mass. The Earth has a large mass, so the acceleration from you pulling on the Earth is small.

name mass (kg) radius (km)
Sun 2.00 × 1030 695 700
Mercury 3.301 × 1023 2440
Venus 4.867 × 1024 6052
Earth 5.972 × 1024 6371
Moon 7.346 × 1022 1737
Mars 6.417 × 1023 3390
Ceres 9.384 × 1020 470
Jupiter 1.899 × 1027 70 000
Saturn 5.685 × 1026 58 232
Uranus 8.68 × 1025 25 362
Neptune 1.024 × 1026 24 622

Example: Find the force of gravity between the Earth and the Moon. The distance between them is 384 403 km.
solution $$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (7.346 \times 10^{22})}{(3.844 \times 10^{8})^{2}}$$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (7.346 \times 10^{22})}{14.78 \times 10^{16}}$$ $$ F = \frac{6.674 \times 5.972 \times 7.346}{14.78} \times \frac{10^{-11}10^{24}10^{22}}{10^{16}}$$ $$ F = 19.798 \times 10^{19} \, \mathrm{N}$$
Example: Find the force of gravity between the Earth and the Sun. The distance between them is 149.6 billion m.
solution $$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (2.00 \times 10^{30})}{(149.6 \times 10^{9})^{2}}$$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (2.00 \times 10^{30})}{22380 \times 10^{18}}$$ $$ F = 3.561 \times 10^{22} \, \mathrm{N}$$
Example: Find the force of gravity between the Earth and a 100 kg person that is 10 000 000 m from the center of the Earth.
solution $$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24})(100)}{ 10\,000\,000^{2}}$$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24})(100)}{ 10^{14}}$$ $$ F = 398.57 \, \mathrm{N}$$
Example: How massive must an object be in order to feel a force of 100 N at a distance of 10 000 000 m from the center of the Earth?
solution $$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ M_{1} = \frac{Fr^{2}}{GM_{2}}$$ $$ M_{1} = \frac{(100)(10\,000\,000)^{2}}{(6.674 \times 10^{-11})(5.972 \times 10^{24})}$$ $$ M_{1} = \frac{(100)(10^{14})}{(6.674 \times 10^{-11})(5.972 \times 10^{24})}$$ $$ M_{1} = 25.01 \, \mathrm{kg}$$
Halley Jupiter Saturn Uranus Neptune Example: When it is closest to the Sun on its 75 year orbit, Halley's Comet feels a force of gravity from the Sun of 3.65 × 1012 N. Calculate its distance from the Sun using the comet's mass of 2.2 × 1014 kg.
solution $$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ r^{2} = \frac{GM_{1}M_{2}}{F} $$ $$ r^{2} = \frac{(6.674 \times 10^{-11})(2.00 \times 10^{30})(2.2 \times 10^{14})}{3.65 \times 10^{12}} $$ $$ \sqrt{r^{2}} = \sqrt{8.04 \times 10^{21}} $$ $$ r = 8.97 \times 10^{10}\,\mathrm{m} $$
$$G = 6.674 × 10^{-11} $$ Question: Notice that universal gravitation constant is very small . Out of the four fundamental forces, gravity is by far the weakest. If gravity is so weak why do we notice its effects so easily?
solution

The force of gravity scales with distance and mass. The Earth is very close and very massive, so it's gravity is large enough to feel.

The force of gravity is very weak though. If gravity were stronger we might notice the pull from human sized objects.

Gravitational Acceleration

It is useful to adapt the universal gravitation equation to predict acceleration. To find acceleration we just need to divide an object's gravitational force by its mass.

derivation of universal gravitational acceleration $$ F = mg $$ $$ \frac{F}{m} = g $$

Newton's second law tells us we can replace F/M with acceleration.

$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ \frac{F}{M_{2}} = \frac{GM_{1}}{r^{2}} $$ $$ g = \frac{GM_{1}}{r^{2}} $$
M g r

$$ g = \frac{GM}{r^{2}} $$

\(g\) = acceleration of gravity [m/s²] vector
\(G\) = \(\small 6.674 \times 10^{-11}\) = universal gravitation constant [m³/kg/s²]
\(M\) = mass of the body pulling [kg, kilograms]
(not the body experiencing the acceleration)
\(r\) = distance between the center of each mass [m, meters]

M g

The acceleration vector is pointed towards the center of the mass producing the acceleration.

The mass of the body being accelerated isn't used in this equation. Use the mass of the body producing the acceleration. To find the acceleration of objects on Earth use Earth's mass.

The simulation below shows a vector field. Each vector shows the gravitational acceleration potentially felt at that location. These diagrams are helpful for predicting how a particle will accelerate.

masses =
Example: Find the acceleration of gravity for an object on the surface of Earth.
Is it really 9.8 m/s²?
Local Massive Objects Data Table
name mass (kg) radius (km)
Sun 2.00 × 1030 695 700
Mercury 3.301 × 1023 2440
Venus 4.867 × 1024 6052
Earth 5.972 × 1024 6371
Moon 7.346 × 1022 1737
Mars 6.417 × 1023 3390
Jupiter 1.899 × 1027 70 000
Saturn 5.685 × 1026 58 232
Uranus 8.68 × 1025 25 362
Neptune 1.024 × 1026 24 622
solution $$ r = 6\,371\,000 \, \mathrm{m} $$ $$ g = \frac{GM}{r^{2}}$$ $$ g = \frac{(6.674\times 10^{-11})(5.972\times 10^{24})}{(6.371\times10^{6})^{2}}$$ $$ g = \frac{(6.674\times 10^{-11})(5.972\times 10^{24})}{40.590\times10^{12}} $$ $$ g =\frac{(6.674)(5.972)}{40.590}\times 10^{-11+24-12}$$ $$ g=0.981\,95 \times 10^{1}$$ $$ g=9.8195 \, \mathrm{\frac{m}{s^{2}}}$$
Example: Find how far away from the Earth you need to be to only accelerate at half of 9.8 m/s².
solution $$ g = \frac{GM}{r^{2}} $$ $$ r^{2} = \frac{GM}{g} $$ $$ r^{2} = \frac{(6.674\times 10^{-11})(5.972\times 10^{24})}{9.8 \times 0.5} $$ $$ r = 9\,160\,226 \,\mathrm{m} = 9160 \,\mathrm{km} $$ $$\text{distance above Earth's surface}$$ $$ 9160\, \mathrm{km} - 6371\,\mathrm{km} = 2789 \,\mathrm{km}$$
Example: Mars has two very small moons, Phobos and Deimos. Phobos has a surface gravity of 0.0057 m/s² and a surface radius of 11 266 m. Calculate the mass of Phobos. (Does your answer agree with wikipedia?)
solution $$ g = \frac{GM}{r^{2}} $$ $$ M = \frac{gr^2}{G}$$ $$ M = \frac{(0.0057)(11\,266)^2}{6.674\times 10^{-11}}$$ $$M = 1.08 \times 10^{16}\,\mathrm{kg}$$

Inverse-Square Law (1/r²)

All particles are attracted to each other, but the attraction is divided by the distance squared. Physical laws that diminish at 1/r² are common in nature because of how signals spread out in 3 dimensions. If you threw darts in random directions, the chance of hitting your target would obey this rule.

Question: What distance between masses produces a force of zero?
answer

As the distance approaches infinity, the force approaches zero.

The effects of gravity can be felt at any real distance. Astronomers see gravitation between our galaxy, the Milky Way, and the Andromeda galaxy at a distance of 2.5 million light years (1022 m)

Question: What happens to the force of gravity as the distance between masses approaches zero?
answer

The force rises towards infinity as the distance approaches zero.

When matter gets very dense, a black hole forms. Understanding gravity at distances near zero require using general relativity and quantum physics at the same time. Currently these two theories are not compatible, but we know that some strange things would happen. Time would slow down, and it would become very difficult for anything to escape.

Question: What else, besides gravity, might follow an inverse square law?
answer

Anything that spreads out in 3 dimensions will follow this law.

  • Light
  • Sound
  • Randomly throwing things, like darts.
    • Example: If you triple the distance between two massive objects, what happens to their force of gravity? What about ten times the distance?
    solution

    This is easier to understand with some made up numbers. Set the masses and G to equal 1 since they aren't changing.

    $$F = \frac{G M_1 M_2}{r^2} \quad \to \quad F = \frac{1}{r^2}$$
    $$\text{\underline{triple}}$$ $$r = 3$$ $$ F = \frac{1}{r^2}$$ $$ F = \frac{1}{3^2}$$ $$ F = \frac{1}{9}$$
    $$\text{\underline{ten times}}$$ $$r = 10$$ $$ F = \frac{1}{r^2}$$ $$ F = \frac{1}{10^2}$$ $$ F = \frac{1}{100}$$

    As the distance between two masses increases, the force of gravity decreases.

    name mass (kg) radius (km) g (m/s²)
    		Mercury 3.301 × 1023 2440 3.7
    		Venus 4.867 × 1024 6052 8.9
    		Earth 5.972 × 1024 6371 9.8
    		Mars 6.417 × 1023 3390 3.7
    Question: Which terrestrial planet is being graphed?
    strategy

    Hover your mouse over the graph. Move your mouse horizontally to check the radius for each planet in the chart above. If the acceleration and the radius match, it is the correct planet.

    answer

    name mass (kg) radius (km) g (m/s²)
    		Jupiter 1.899 × 1027 70 000 ?
    		Saturn 5.685 × 1026 58 232 ?
    		Uranus 8.68 × 1025 25 362 ?
    		Neptune 1.024 × 1026 24 622 ?
    Question: Which gas giant is being graphed? You need to do math for this one.
    answer

    Questions: Imagine you could to dig into the center of the Earth. How would the acceleration of gravity change as you went deeper? Would it increase, decrease, or stay the same?
    answer

    As you go deeper into the Earth you feel less gravity. There is mass both above and below, they pull in opposite directions and cancel out. You can't feel opposing forces of gravity, because gravity pulls on your whole body evenly.

    Using a model of the Earth with constant density the gravity decreases linearly. At 50% to the center of the Earth the gravity is 50% of 9.8 m/s². At the center gravity is zero.

    Gravity Acceleration of Earth This svg graphic is to edit with an text editor. Please do not overwrite this file by saving with an image editor. ---------------- Source of PREM: http://geophysics.ou.edu/solid_earth/prem.html Linear density: line with constant rise Source of constant density: copied from http://commons.wikimedia.org/wiki/File:EarthGravityPREM.jpg; the base source or calculation is not stated there Space: g1 * r1^2 = g0 * r0^2 0 2 4 6 8 10 12 14 radius in 1000 km 0 2 4 6 8 10 12 acceleration in m/s 2 PREM Linear density Constant density Free-fall acceleration of Earth Inner Core Outer Core Lower Mantle Upper Mantle Space

    Earth's actual gravity according to the Preliminary Reference Earth Model (PREM) is more complex. This is because the density changes with each layer, and increases towards the center.

    Gravitational Potential Energy

    Our old gravitational potential energy equation, U=mgh, can be made more accurate if we replace g = 9.8 with a calculated gravitational acceleration. This version of gravitational potential energy now works beyond Earth's surface.

    derivation of universal gravitational potential energy $$U_{g} = mgh \quad g = \color{blue}{\frac{GM}{r^{2}}} $$ $$U_{g} = m{\color{blue}{\frac{GM}{r^{2}}}}h $$

    If we define h to be zero when the two masses are zero distance apart, we can rename h to r.

    $$U_{g} = \frac{GM_{1}M_{2}}{r^{2}}r$$ $$U_{g} = \frac{GM_{1}M_{2}}{r} $$
    When distance is very big the energy goes to zero, so it makes sense to choose the zero of this gravitational potential energy at an infinite distance away. This means that as we bring a mass closer to another mass we have negative potential energy. $$U_{g} = -\frac{GM_{1}M_{2}}{r} $$

    Here is a more complete derivation using calculus.

    M 1 M 2 r

    $$U_{g} = -\frac{GM_{1}M_{2}}{r} $$

    \(U_g\) = gravitational potential energy [J, joules]
    \(G\) = 6.67408 × 10-11 = universal gravitation constant [N(m/kg)²]
    \(M\) = mass [kg, kilograms]
    \(r\) = distance between the center of each mass [m, meters]

    M 1 M 2

    What is the gravitational potential energy when two masses are at zero distance away?

    What is the gravitational potential energy when two masses are at an infinite distance away?

    masses =

    Energy is a scalar, not a vector. This means that when we calculate gravitational potential energy it has no direction. You can see the potential energy in the simulation below as a scalar field. Think of the reddish regions as being deeper into the gravity well.

    Example: Calculate the gravitational potential energy between two 100 000 kg masses when there is only 2 m between the center of each mass.
    solution $$U_{g} = -\frac{GM_{1}M_{2}}{r}$$ $$U_{g} = -\frac{(6.674 \times 10^{-11}) (100\,000)(100\,000)}{2}$$ $$U_{g} = -0.33\,\mathrm{J}$$

    The energy is negative because it would take positive work to separate the masses.

    Example: Two 100 000 kg masses are 2 meters apart. How much work would it take to bring them to 10 m apart?
    strategy

    Calculate the gravitational potential energy at each distance. The change in energy is the work.

    solution $$U_{i} = -\frac{GM_{1}M_{2}}{r}$$ $$U_{i} = -\frac{(6.674 \times 10^{-11})(100\,000)(100\,000)}{2}$$ $$U_{i} = -0.33\,\mathrm{J}$$
    $$U_{f} = -\frac{(6.674 \times 10^{-11})(100\,000)(100\,000)}{10}$$ $$U_{f} = -0.068\,\mathrm{J}$$

    Work is a change in energy, so we can subtract the final energy from the initial.

    $$W = \Delta U = U_{f} - U_{i} $$ $$W = (-0.068) - (-0.33)$$ $$W = 0.262 \, \mathrm{J}$$
    Example: A 2000 kg spaceship starts at rest 20 000 km from the surface of Earth. How much kinetic energy will the ship have after it falls down to 10 000 km from the surface of Earth?
    strategy

    Use conservation of energy. Set the initial kinetic and gravitational potential equal to the final kinetic and gravitational potential.

    solution $$E_{i} = E_{f}$$ $$U_{gi} = U_{gf} + K$$ $$ K = U_{gi} - U_{gf}$$ $$K = -\frac{GM_{1}M_{2}}{r}+\frac{GM_{1}M_{2}}{r}$$ $$K = -\frac{(6.674\times 10^{-11})(5.972\times 10^{24})(2000)}{6\,371\,000 + 20\,000\,000}$$ $$+\frac{(6.674\times 10^{-11})(5.972\times 10^{24})(2000)}{6\,371\,000 + 10\,000\,000}$$ $$K = -3.02 \times 10^{10}+4.86 \times 10^{10} $$ $$K = 1.85 \times 10^{10} \, \mathrm{J}$$
    Example: Find the minimum escape velocity for a 100 kg person on Earth.
    strategy

    Use conservation of energy to find the energy needed to bring both the kinetic and potential energy to zero.

    solution $$E_{i} = E_{f}$$ $$U_{gi} + K = U_{gf} + K$$ $$U_{gi} + K = 0$$ $$K = -U_{gi}$$ $$(1/2)M_{2}v^2 = \frac{GM_{1}M_{2}}{r}$$ $$(1/2)v^2 = \frac{GM_{1}}{r}$$ $$\boxed{v^2 = \frac{2GM_{1}}{r}}$$ $$v = \sqrt{\frac{2(6.674\times 10^{-11}) (5.972 \times 10 ^{24})}{6\,371\,000}}$$ $$v = 11\,183 \, \mathrm{\tfrac{m}{s}}$$

    Example: Find the minimum escape velocity on Phobos.
    solution $$v^2 = \frac{2GM_{1}}{r}$$ $$v^2 = \frac{2(6.674\times 10^{-11})(1.1 \times 10^{16})}{11200}$$ $$v = \sqrt{\frac{2(6.674\times 10^{-11})(1.1 \times 10^{16})}{11200}}$$ $$v = 11.45\, \mathrm{\tfrac{m}{s}}$$
    Use the mouse to move the camera. Double click for full screen. In the simulation above, gravitational potential energy is represented as warping a 2-D fabric into a 3rd dimension. This is similar to how gravity is thought of in general relativity.